Do You Read Left to Right or Vice Vresa for Binary Nunmbers

Binary Tree (with Coffee Lawmaking)
![]()
by Sven Woltmann – May 28, 2021
Ii of the most important topics in computer science are sorting and searching data sets. A data structure often used for both is the binary tree and its concrete implementations binary search tree and binary heap. In this article, y'all will learn: You can find the source code for the article in this GitHub repository. A binary tree is a tree data structure in which each node has at most ii child nodes. The child nodes are chosen left child and right child. As an instance, a binary tree looks similar this: As a developer, you should know the following terms: The post-obit image shows the same binary tree information structure every bit before, labeled with node types, node depth, and binary tree height. Before we get to the implementation of binary copse and their operations, allow'due south first briefly look at some special binary tree types. In a full binary tree, all nodes have either no children or two children. In a consummate binary tree, all levels, except possibly the last one, are completely filled. If the last level is not completely filled, then its nodes are arranged equally far to the left equally possible. A perfect binary tree is a total binary tree in which all leaves have the same depth. A perfect binary tree of height h has n = 2h+1-1 nodes and l = 2h leaves. At the height of 3, that's xv nodes, viii of which are leaves. In a counterbalanced binary tree, each node's left and right subtrees differ in elevation by at almost one. In a sorted binary tree (also known every bit ordered binary tree), the left subtree of a node contains merely values less than (or equal to) the value of the parent node, and the right subtree contains only values greater than (or equal to) the value of the parent node. Such a data construction is also called a binary search tree. For the binary tree implementation in Java, we kickoff define the information construction for the nodes (class Node in the GitHub repository). For simplicity, nosotros use The parent reference is non mandatory for storing and displaying the tree. Yet, it is helpful – at to the lowest degree for sure types of binary trees – when deleting nodes. The binary tree itself initially consists only of the interface BinaryTree and its minimal implementation BaseBinaryTree, which initially contains only a reference to the root node: Why nosotros bother to define an interface hither will become apparent in the further course of the tutorial. The binary tree data structure is thus fully divers. An essential operation on binary trees is the traversal of all nodes, i.e., visiting all nodes in a particular club. The most common types of traversal are: In the following sections, you will see the different types illustrated by the post-obit example: We implement the visiting during traversal using the visitor blueprint pattern, i.due east., we create a company object which we pass to the traversal method. In depth-showtime search (DFS), we perform the post-obit iii operations in a specific guild: The standard sequences are: In pre-order traversal (also known as NLR), traversing is performed in the following club: The nodes of the case tree are visited in the following club, as shown in the diagram below: 3→1→13→10→eleven→16→15→2 The code for this is adequately unproblematic (DepthFirstTraversalRecursive form, starting at line 21): You tin either invoke the method directly – in which case you lot must pass the the root node to it – or via the non-static method This requires creating an example of An iterative implementation is as well possible using a stack (grade DepthFirstTraversalIterative from line 20). The iterative implementations are pretty complex, which is why I practice not print them here. You can read why I utilise In mail service-social club traversal (also known as LRN), traversing is performed in the following order: In this case, the nodes of the example tree are visited in the following order: 13→one→xi→15→2→16→x→3 You can find the lawmaking in DepthFirstTraversalRecursive starting at line 42: You lot tin can find the iterative implementation, which is fifty-fifty more than complicated for post-order traversal than for pre-gild traversal, in DepthFirstTraversalIterative starting at line 44. In-guild traversal (besides known as LNR) traverses the tree in the post-obit society: The nodes of the case tree are visited in the following guild: xiii→1→3→11→ten→xv→sixteen→ii You will find the recursive lawmaking in DepthFirstTraversalRecursive starting at line 62: See DepthFirstTraversalIterative starting at line 69 for the iterative implementation of in-social club traversal. In a binary search tree, in-order traversal visits the nodes in the order in which they are sorted. Contrary in-order traversal (also known as RNL) traverses the tree in the post-obit reverse order: The nodes of the sample tree are visited in opposite order to the in-lodge traversal: 2→16→15→x→11→3→1→13 You will find the recursive code in DepthFirstTraversalRecursive starting at line 83: You tin discover the iterative implementation of reverse in-gild traversal in DepthFirstTraversalIterative starting at line 89. In a binary search tree, contrary in-order traversal visits the nodes in descending sort order. In breadth-first search (BFS) – too chosen level-order traversal – nodes are visited starting from the root, level by level, from left to correct. Level-order traversal results in the following sequence: 3→1→ten→13→11→16→xv→2 To visit the nodes in level-order, we need a queue in which we first insert the root node and and then repeatedly remove the first element, visit it, and add its children to the queue – until the queue is empty once again. You can notice the code in the BreadthFirstTraversal class: You tin discover examples for invoking all traversal types in the Besides traversal, other bones operations on binary trees are the insertion and deletion of nodes. Search operations are provided by special binary trees such as the binary search tree. Without special backdrop, nosotros tin search a binary tree only by traversing over all nodes and comparing each with the searched element. When inserting new nodes into a binary tree, nosotros have to distinguish different cases: Es ist leicht einen neuen Knoten an ein Blatt oder ein Halbblatt anzuhängen. Hierzu müssen wir lediglich dice It is like shooting fish in a barrel to append a new node to a leaf or one-half leaf. To do this, we but need to set the But how do you lot go about inserting a node between an inner node and one of its children? This is only possible by reorganizing the tree. How exactly the tree is reorganized depends on the concrete type of binary tree. In this tutorial, we implement a very simple binary tree and proceed as follows for the reorganization: The following diagram shows the 2d example: We insert the new node Due north between P and R: This is – as mentioned – a very elementary implementation. In the example above, this results in a highly unbalanced binary tree. Specific binary trees take a unlike approach here to maintain a tree structure that satisfies the particular properties of the binary tree in question (sorting, balancing, etc.). Hither you tin can see the lawmaking for inserting a new node with the given (The switch expression with the curly braces was introduced in Java 12/13.) In the Too, when deleting a node, nosotros have to distinguish different cases. If the node N to be deleted is a leafage, i.e., has no children itself, then the node is simply removed. To exercise this, we check whether the node is the left or right child of the parent P and set P'due south If the node N to be deleted has a child C itself, then the child moves upward to the deleted position. Again, we check whether node North is the left or right child of its parent P. And so, accordingly, nosotros set up the How to proceed if you want to delete a node with two children? This requires a reorganization of the binary tree. Analogous to insertion, there are once again dissimilar strategies for deletion – depending on the concrete type of binary tree. In a heap, for example, the last node of the tree is placed at the position of the deleted node and so the heap is repaired. We utilize the following easy-to-implement variant for our tutorial: We tin run into clearly how this strategy leads to a severely unbalanced binary tree. Specific implementations like the binary search tree and the binary heap, therefore, take more circuitous strategies. The following method (class SimpleBinaryTree starting at line 71) removes the passed node from the tree. Corresponding comments marker cases A, B, and C. The In instance the deleted node is the root node, we simply replace the In case C (deleting a node with two children), the tree is reorganized as described in the previous section. This is done in the carve up method In the Finally, I want to show you lot an alternative representation of the binary tree: storing it in an array. The array contains as many elements every bit a perfect binary tree of the height of the binary tree to be stored, i.eastward., twoh+1-1 elements for height h (in the following paradigm: 7 elements for height 2). The nodes of the tree are sequentially numbered from the root downwards, level past level, from left to right, and mapped to the array, as shown in the following illustration: For a complete binary tree, we can trim the array appropriately – or shop the number of nodes equally an additional value. Storing a binary tree as an assortment has the following advantages: Confronting these, 1 must counterbalance the following disadvantages: In this article, you learned what a binary tree is, what types of binary trees exist, what operations you can utilize to binary trees, and how to implement a binary tree in Java. If you lot liked the commodity, feel free to share it using one of the share buttons below. Do you want to exist informed when the next commodity is published? So click here to sign up for the HappyCoders newsletter.
Binary Tree Definition
Binary Tree Example
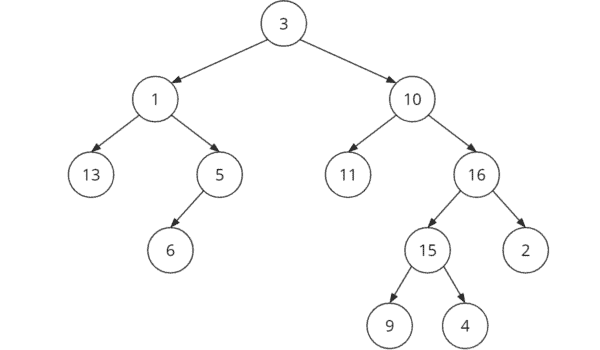
Binary Tree Terminology

Binary Trees Properties
Full Binary Tree

Consummate Binary Tree

Perfect Binary Tree

Counterbalanced Binary Tree

Sorted Binary Tree
Binary Tree in Java
int primitives equally node information. We can, of course, use any other or a generic data blazon; yet, with an int, the code is more readable – and that is most of import for this tutorial. public course Node { int data; Node left; Node right; Node parent; public Node (int information) { this.data = information; } } public interface BinaryTree { Node getRoot () ; } public course BaseBinaryTree implements BinaryTree { Node root; @Override public Node getRoot () { return root; } } Binary Tree Traversal

Depth-First Search in a Binary Tree
Binary Tree Pre-Guild Traversal
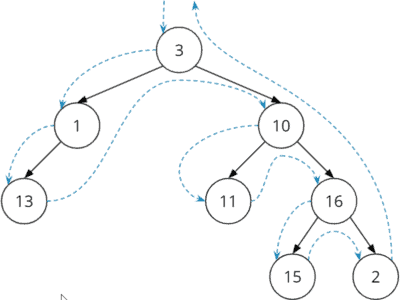
private void traversePreOrder (Node node, NodeVisitor visitor) { if (node == naught) { render; } visitor.visit(node); traversePreOrder(node.left, visitor); traversePreOrder(node.correct, visitor); } traversePreOrder() in the aforementioned class (DepthFirstTraversalRecursive, starting at line 17): public void traversePreOrder (NodeVisitor company) { traversePreOrder(tree.getRoot(), company); } DepthFirstTraversalRecursive, passing a reference to the binary tree to the constructor: new DepthFirstTraversalRecursive(tree).traversePreOrder(visitor); ArrayDeque instead of Stack in iterative tree traversals hither: Why you lot should not use Stack. Binary Tree Post-Guild Traversal

public static void traversePostOrder (Node node, NodeVisitor company) { if (node == null) { return; } traversePostOrder(node.left, visitor); traversePostOrder(node.right, visitor); visitor.visit(node); } Binary Tree In-Order Traversal

public static void traverseInOrder (Node node, NodeVisitor visitor) { if (node == null) { render; } traverseInOrder(node.left, company); company.visit(node); traverseInOrder(node.right, visitor); } Binary Tree Contrary In-Order Traversal

public static void traverseReverseInOrder (Node node, NodeVisitor visitor) { if (node == null) { render; } traverseReverseInOrder(node.correct, company); visitor.visit(node); traverseReverseInOrder(node.left, visitor); } Binary Tree Level-Lodge Traversal

public static void traverseLevelOrder (Node root, NodeVisitor visitor) { if (root == zero) { render; } Queue<Node> queue = new ArrayDeque<>(); queue.add(root); while (!queue.isEmpty()) { Node node = queue.poll(); visitor.visit(node); if (node.left != nothing) { queue.add(node.left); } if (node.right != zip) { queue.add together(node.right); } } } traverseTreeInVariousWays() method of the Example1 class. Binary Tree Operations
Insertion of a Node
Case A: Inserting a Node Beneath a (Half) Leaf
left- oder right-Referenz des Parent-Knotens P, an den wir den neuen Knoten North anhängen wollen, auf den neuen Knoten setzen. Wenn wir auch mit parent-Referenzen arbeiten, müssen wir diese im neuen Knoten Due north auf den Parent-Knoten P setzen.left or correct reference of the parent node P, to which we desire to suspend the new node North, to the new node. If nosotros are working with a parent reference, we need to set the new node's parent reference to P.

Case B: Inserting a Node Between Inner Node and Its Kid


Inserting a Binary Tree Node – Java Source Code
data below the given parent node to the specified side (left or right) using the reorganization strategy divers in the previous section (class SimpleBinaryTree starting at line 18). public Node insertNode (int data, Node parent, Side side) { var node = new Node(information); node.parent = parent; switch (side) { example LEFT -> { if (parent.left != null) { node.left = parent.left; node.left.parent = node; } parent.left = node; } case Right -> { if (parent.correct != zip) { node.right = parent.right; node.right.parent = node; } parent.right = node; } default -> throw new IllegalStateException(); } return node; } createSampleTree() method of the Example1 class, you tin can run into how to create the sample binary tree from the beginning of this article. Deletion of a Node
Case A: Deleting a Node Without Children (Foliage)
left or right reference to zero accordingly.
Case B: Deleting a Node With One Child (Half Leaf)
left or correct reference of P to N's child C (the previous grandchild) – and C's parent reference to N'due south parent P (the previous grandparent node).
Instance C: Deleting a Node With Two Children


Deleting a Tree Node – Java Source Code
public void deleteNode (Node node) { if (node.parent == cypher && node != root) { throw new IllegalStateException("Node has no parent and is not root"); } // Example A: Node has no children --> set up node to null in parent if (node.left == goose egg && node.right == nada) { setParentsChild(node, nil); } // Case B: Node has one kid --> replace node by node's child in parent // Example B1: Node has merely left kid else if (node.right == cipher) { setParentsChild(node, node.left); } // Case B2: Node has only right child else if (node.left == zilch) { setParentsChild(node, node.right); } // Case C: Node has two children else { removeNodeWithTwoChildren(node); } // Remove all references from the deleted node node.parent = null; node.left = null; node.right = null; } setParentsChild() method checks whether the node to be deleted is the left or right child of its parent node and replaces the corresponding reference in the parent node with the child node. kid is null if the node to be deleted has no children, and appropriately, the child reference in the parent node is set to goose egg.root reference. individual void setParentsChild (Node node, Node child) { // Node is root? Has no parent, set root reference instead if (node == root) { root = kid; if (child != nil) { child.parent = null; } return; } // Am I the left or right child of my parent? if (node.parent.left == node) { node.parent.left = child; } else if (node.parent.correct == node) { node.parent.right = kid; } else { throw new IllegalStateException( "Node " + node.data + " is neither a left nor a right kid of its parent " + node.parent.information); } if (child != null) { child.parent = node.parent; } } removeNodeWithTwoChildren(): private void removeNodeWithTwoChildren (Node node) { Node leftTree = node.left; Node rightTree = node.correct; setParentsChild(node, leftTree); // observe correct-most child of left tree Node rightMostChildOfLeftTree = leftTree; while (rightMostChildOfLeftTree.right != nada) { rightMostChildOfLeftTree = rightMostChildOfLeftTree.correct; } // suspend right tree to right child rightMostChildOfLeftTree.right = rightTree; rightTree.parent = rightMostChildOfLeftTree; } deleteSomeNodes() method of the Example1 class, you tin see how some nodes of the instance tree are deleted again. Array Representation of a Binary Tree

Advantages and Disadvantages of the Array Representation
For a node at index i,
Summary
Source: https://www.happycoders.eu/algorithms/binary-tree-java/
0 Response to "Do You Read Left to Right or Vice Vresa for Binary Nunmbers"
Post a Comment