Draw a Parse Tree for Input String Aabbb

Parse Tree-

• The process of deriving a string is called as derivation.
• The geometrical representation of a derivation is called as a parse tree or derivation tree.

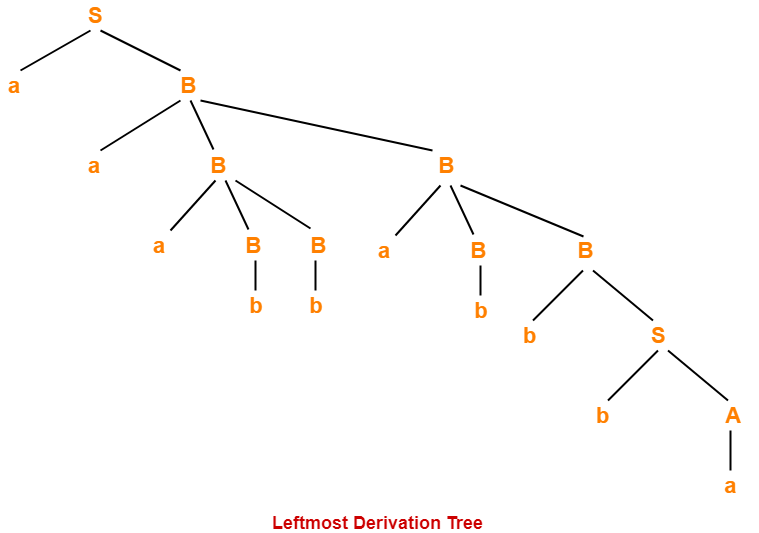
1. Leftmost Derivation-

• The process of deriving a string by expanding the leftmost non-terminal at each step is called as leftmost derivation.
• The geometrical representation of leftmost derivation is called as a leftmost derivation tree.

Example-

Consider the following grammar-

S → aB / bA

S → aS / bAA / a

B → bS / aBB / b

(Unambiguous Grammar)

Let us consider a string w = aaabbabbba

Now, let us derive the string w using leftmost derivation.

Leftmost Derivation-

S → aB

→ aaBB (Using B → aBB)

→ aaaBBB (Using B → aBB)

→ aaabBB (Using B → b)

→ aaabbB (Using B → b)

→ aaabbaBB (Using B → aBB)

→ aaabbabB (Using B → b)

→ aaabbabbS (Using B → bS)

→ aaabbabbbA (Using S → bA)

→ aaabbabbba (Using A → a)

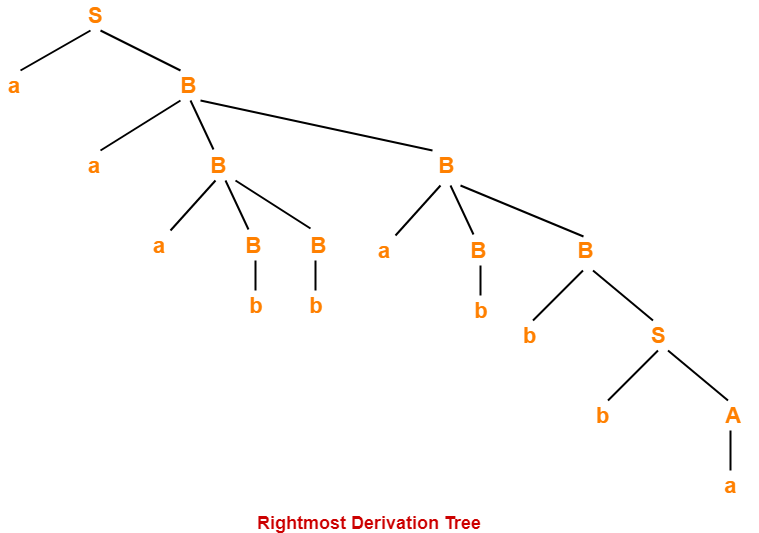
2. Rightmost Derivation-

• The process of deriving a string by expanding the rightmost non-terminal at each step is called as rightmost derivation.
• The geometrical representation of rightmost derivation is called as a rightmost derivation tree.

Example-

Consider the following grammar-

S → aB / bA

S → aS / bAA / a

B → bS / aBB / b

(Unambiguous Grammar)

Let us consider a string w = aaabbabbba

Now, let us derive the string w using rightmost derivation.

Rightmost Derivation-

S → aB

→ aaBB (Using B → aBB)

→ aaBaBB (Using B → aBB)

→ aaBaBbS (Using B → bS)

→ aaBaBbbA (Using S → bA)

→ aaBaBbba (Using A → a)

→ aaBabbba (Using B → b)

→ aaaBBabbba (Using B → aBB)

→ aaaBbabbba (Using B → b)

→ aaabbabbba (Using B → b)

NOTES

• For unambiguous grammars, Leftmost derivation and Rightmost derivation represents the same parse tree.
• For ambiguous grammars, Leftmost derivation and Rightmost derivation represents different parse trees.

Here,

• The given grammar was unambiguous.
• That is why, leftmost derivation and rightmost derivation represents the same parse tree.

Leftmost Derivation Tree = Rightmost Derivation Tree

Also Read- Ambiguous Grammar

Properties Of Parse Tree-

• Root node of a parse tree is the start symbol of the grammar.
• Each leaf node of a parse tree represents a terminal symbol.
• Each interior node of a parse tree represents a non-terminal symbol.
• Parse tree is independent of the order in which the productions are used during derivations.

Yield Of Parse Tree-

• Concatenating the leaves of a parse tree from the left produces a string of terminals.
• This string of terminals is called as yield of a parse tree.

PRACTICE PROBLEMS BASED ON DERIVATIONS AND PARSE TREE-

Problem-01:

Consider the grammar-

S → bB / aA

A → b / bS / aAA

B → a / aS / bBB

For the string w = bbaababa, find-

1. Leftmost derivation
2. Rightmost derivation
3. Parse Tree

Solution-

1. Leftmost Derivation-

S → bB

→ bbBB (Using B → bBB)

→ bbaB (Using B → a)

→ bbaaS (Using B → aS)

→ bbaabB (Using S → bB)

→ bbaabaS (Using B → aS)

→ bbaababB (Using S → bB)

→ bbaababa (Using B → a)

2. Rightmost Derivation-

S → bB

→ bbBB (Using B → bBB)

→ bbBaS (Using B → aS)

→ bbBabB (Using S → bB)

→ bbBabaS (Using B → aS)

→ bbBababB (Using S → bB)

→ bbBababa (Using B → a)

→ bbaababa (Using B → a)

3. Parse Tree-

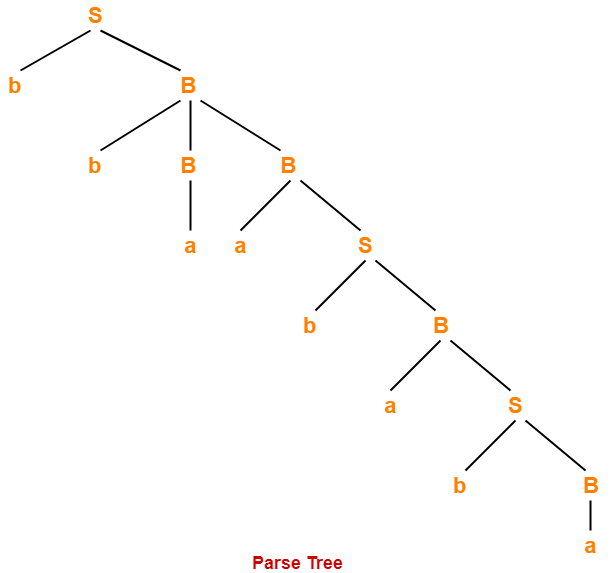
• Whether we consider the leftmost derivation or rightmost derivation, we get the above parse tree.
• The reason is given grammar is unambiguous.

Problem-02:

Consider the grammar-

S → A1B

A → 0A / ∈

B → 0B / 1B / ∈

For the string w = 00101, find-

1. Leftmost derivation
2. Rightmost derivation
3. Parse Tree

Solution-

1. Leftmost Derivation-

S → A1B

→ 0A1B (Using A → 0A)

→ 00A1B (Using A → 0A)

→ 001B (Using A → ∈)

→ 0010B (Using B → 0B)

→ 00101B (Using B → 1B)

→ 00101 (Using B → ∈)

2. Rightmost Derivation-

S → A1B

→ A10B (Using B → 0B)

→ A101B (Using B → 1B)

→ A101 (Using B → ∈)

→ 0A101 (Using A → 0A)

→ 00A101 (Using A → 0A)

→ 00101 (Using A → ∈)

3. Parse Tree-

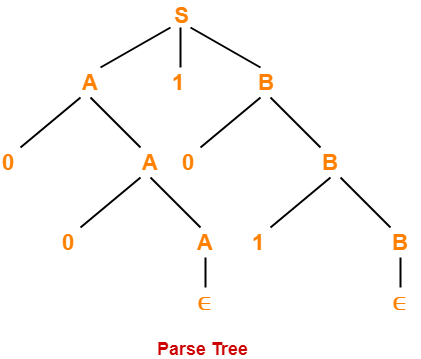
• Whether we consider the leftmost derivation or rightmost derivation, we get the above parse tree.
• The reason is given grammar is unambiguous.

To gain better understanding about Derivations and Parse Tree,

Watch this Video Lecture

Next Article- Elimination of Left Recursion

Get more notes and other study material of Theory of Automata and Computation.

Watch video lectures by visiting our YouTube channel LearnVidFun.

Summary

Article Name

Parse Tree | Derivations | Automata

Description

In automata, derivation is a process of deriving a string. Parse tree or Derivation tree is the geometrical representation of a derivation. Leftmost Derivation and Rightmost Derivation are the two types of derivation.

Author

Akshay Singhal

Publisher Name

Gate Vidyalay

Publisher Logo

kuesterreatunat.blogspot.com

Source: https://www.gatevidyalay.com/parse-tree-derivations-automata/

Share this post